Add & Norm：对残差连接深入解析（一）

本文发表于 206 天前，其中的信息可能已经事过境迁

写在前面

在我最早学习LLMs时候，残差连接这个词看着就很高大上，让我望而生畏，极大的延缓了我系统的学习的进度。但是，因为这样那样的原因，最终我还是恶补了各种知识。学完之后觉得也就那样了，所以，我希望初学者看到tranformer里藏着这样一个部分的时候，可以不用过多担心，直接开始看。

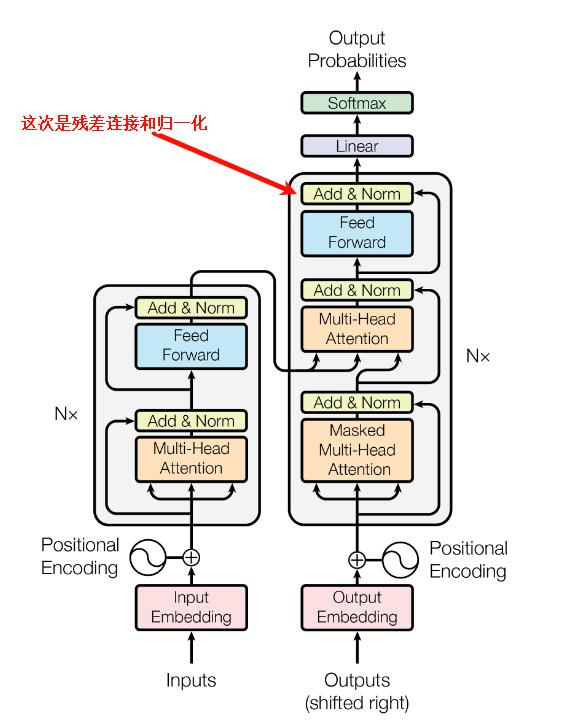
transformer结构

Add & norm介绍

Add Norm 是残差连接（Add）和归一化（Norm）的组合，常用于深层网络。在 Transformer 中，每个子层，也就是自注意力层和前馈神经网络层之后，都会应用 Add Norm，在朴素的transformer中，一般是先执行残差连接Skip connection，再进行归一化，在这里通常指的是Layer Norm。

在原始的Transformer论文中，采用的是‘Post-LN’结构，即先Add再Norm。但后续研究转而使用‘Pre-LN’结构，本文在介绍Add的时候，依然还是围绕原始的Post-LN结构来解释其设计思想。

Add 的思想源于残差学习，这一思想源于经典的ResNet。其定义是：给定输入 $x$ ，网络层函数 $F (x)$ 的输出不直接作为下一层输入，而是通过一个“捷径”连接与原始输入相加，即输出

\begin{aligned} 残差连接: & y = x + Sublayer (x) \\ 其中 & Sublayer (x) = F_{attn} (x) 或 F_{ffn} (x) \end{aligned}

我们可以简化一下，在这里我们用 $H (x)$ 表示完整的输出，而 $F (x)$ 代表残差信息。

H (x) = F (x) + x

核心思想是，通过这个“捷径“结构，保留原始输入信息。这个结构的改变，让网络不再学习完整的输出 $H (x)$ ，而是学习残差函数 $F (x)$ 。如果 $F (x)$ 能有效学习，则 $H (x)$ 是输入 $x$ 和残差 $F (x)$ 的结合；如果该层没有必要学习，或者会导致学习有害，则让 $F (x) = 0$ ，则输出 $H (x) = x$ ，这个步骤我们称为恒等映射，来确保网络至少不退化。

transformer中的add & norm 代码

python

def transformer_layer(x):
    # 多头注意力 + 残差连接
    attn_out = multi_head_attention(x)
    x = layer_norm(x + attn_out)
    
    # 前馈网络 + 残差连接
    ffn_out = feed_forward_network(x)
    x = layer_norm(x + ffn_out)
    
    return x

信息差

要从根本上了解残差连接，首先让我们从现实世界的概念上去理解什么是信息差。由于整体结构改变，关键在于理解 $F (x)$ 代表什么。这里的 $F (x)$ 不是一个全新的、与 $x$ 无关的上下文信息，而是基于 $x$ 计算出来的“调整量”、“补充信息”或者“从特定角度关注 $x$ 后得到的洞察”。

例子

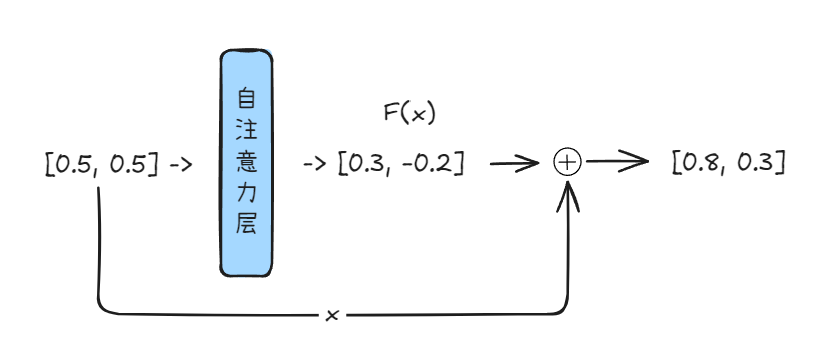
我们用一个高度简化的例子来说明。考虑单词 “bank”，其初始嵌入向量，经过初步训练。x_bank 可能包含了混杂的语义包括：“金融机构”和“河岸”。假设我们将其语义简化为一个二维向量 [金融属性, 地理属性]。它可能与“金融”、“河流”、“存储”等概念都有一定的关联度，已经有了一定的上下文理解，但可能还不够精确。

简化的残差网络的例子

初始状态 x_bank: 假设 x_bank = [0.5, 0.5]，表示模型初步认为两种含义的可能性相当，语义尚不明确。
计算 F(x_bank): 当 “bank” 进入一个自注意力层或者前馈神经网络层，模型会根据当前句子的上下文，例如 “I need to withdraw money from the bank.”进行计算。假设它输出 F(x_bank) = [0.3, -0.2]。
解读 F(x_bank): 这个向量 [0.3, -0.2] 并不直接定义 “bank” 的完整新含义。它传达的是：“基于当前上下文，需要在原始表示 x_bank 的基础上，增强金融属性约 0.3，同时减弱地理属性约 0.2。”
这就是那个关键的“信息差”——需要向理想状态调整的方向和幅度。

H (x_{b a n k}) = F (x_{b a n k}) + x = [0.3, - 0.2] + [0.5, 0.5] = [0.8, 0.3]

H(x): 新的向量 [0.8, 0.3] 显著强化了 “bank” 在当前语境下的金融含义，同时保留了部分地理属性的可能性，但权重降低。F(x_bank) 提供的“信息差”有效地引导了语义的聚焦。

理解信息差

当然，实际情况复杂得多。现实中的词嵌入是高维向量（如 512、768 维），语义信息分布式地编码在各个维度中，难以像二维例子这样直观对应单一属性。相应地， $F (x)$ 学习到的“信息差”也是高维且分布式的。它的核心目标不再是直接输出一个完美的最终答案，而是精准地计算出：为了在当前上下文中获得更优的表示，需要在原始输入 $x$ 的哪些维度上、进行何种程度的调整（增加或减少）。这个“调整量”就是 $F (x)$ 所承载的“信息差”。

为什么这样做比直接设置$H(x)$更好

这里就要提到网络退化和恒等映射这两个概念。

网络退化（Degradation）

网络退化指在极深的神经网络中，简单的堆叠更多层数，不仅无法带来性能提升，反而会导致训练误差上升。最早是何凯明等大佬通过实验发现，当卷积神经网络深度超过20层时，模型性能不升反降。这一现象并非由于过拟合，而是优化困难所致。

理论上来说，一个深层的神经网络，至少应该表现出和浅层相同的效果，但是网络退化这一现象导致一个深层网络反而不如浅层了。

这不是说我们就直接使用浅层网络，深层网络有深层网络的好，但是网络退化这一现象让深层网络失去了作用。既然浅层的时候可以正常学习，那为什么一旦到了某个阈值的深层网络就不行了？

研究者们开始从网络层的角度探究原因，推测可能是一部分层无法有效学习，甚至对整个模型的性能造成了负面影响，从而引发了退化现象。

恒等映射（Identity Mapping）

于是在残差连接中，提出了恒等映射这一思路。当残差函数 $F (x)$ 的输出趋近于零时， $H (x) \approx x$ 。这意味着该残差块近似执行了一个恒等变换，允许信息无损地从输入传播到输出。

这种机制使得网络在训练过程中，若某些层对当前任务贡献甚微或产生负面影响，优化器可以更容易地将这些层的 $F (x)$ 推向零，从而“绕过”这些层，避免了不必要的复杂变换或有害更新，确保深层网络至少能达到其浅层版本的性能。

为什么原来的网络结构没有恒等映射？

严格来说，不是原来的结构没有恒等映射。而在于其学习恒等映射的优化难度。首先，我们要认为 $H (x)$ 可以始终认为是我们要找的最优。

在传统的深度网络架构中，无论是注意力层还是前馈网络层，其设计目标是直接学习一个复杂的目标函数 $H (x)$ 。每一层都肩负着将输入变换为更优表征的责任，力求直接逼近该最优解。

若期望某一层实现恒等映射，即 Layer(x) = x，则该层的参数需要被精确地优化到特定的配置，举例来说， $W$ 趋近单位矩阵 $I$ ， $b$ 趋近零向量。对于通过梯度下降等方法从随机初始化状态开始训练的网络而言，这是一个高度非凸且难以稳定达成的优化目标。

然而，当引入残差连接后，学习范式发生了根本性转变。期望的最优输出 $H (x)$ 被重新参数化为输入 $x$ 与一个待学习的残差函数 $F (x)$ 之和：

H (x) = F (x) + x

在这种框架下，网络层或残差块的学习目标不再是直接拟合完整的 $H (x)$ ，而是学习这个 “信息增量”或“修正量” $F (x) = H (x) - x$ 。

这种学习目标的转换，显著降低了网络层在特定情况下的优化压力。具体来说，传统深层网络中，无用层可能因随机初始化或训练噪声破坏已有特征。残差结构则天然规避此风险，对于当前任务，如果输入 $x$ 本身已经是一个较好的表征，或者某个、某组层对模型的进一步贡献有限甚至可能产生负面影响时，优化器会发现将对应的 $F (x)$ 驱动向零是一个更容易收敛的目标。当 $F (x) \approx 0$ 时，便自然实现了 $H (x) \approx x$ ，即恒等映射。

对于一个自注意力层或者前馈神经网络层，局部来看，它无法感知到整个网络结构。对于它而言输入的只是一个向量，所以它的输出为什么在残差结构下就能逼近信息差？

无论传统网络还是残差网络，单个网络层（Self-Attention/FFN）在训练时接收到的信号是完全相同的：

输入：上游传递的向量 $x$
优化目标：通过梯度下降调整自身参数，使最终损失函数最小化

该层无法感知自身在网络中的位置，更不知道"残差连接"的存在。它只看到输入 $x$ ，并试图生成对最终任务最有帮助的输出。

对于这个问题，熟悉神经网络的同学肯定脱口而出，一切都是因为反向传播和梯度。

\begin{aligned} 输出 & H (x) = F (x) = σ (W x + b) \\ 损失梯度 & \frac{\partial L}{\partial W} = \frac{\partial L}{\partial H} \cdot \frac{\partial H}{\partial W} \end{aligned}

在这个普通结构中， $F (x)$ 层的全部责任就是将输入 $x$ 变换成对最终任务最优的输出 $H (x)$ 。梯度 $\partial L / \partial H$ 会完全传递给 $F$ ，迫使 $F$ 去学习一个完整的、理想的映射。

但是，在引入了 Add & Norm 的残差结构后，情况就不一样了。

\frac{\partial L}{\partial x} = \frac{\partial L}{\partial H} \cdot (1 + \frac{\partial F (x)}{\partial x})

Add的梯度是这样的，这个梯度提供了两个优势：一是对于 $\frac{\partial f (x)}{\partial x}$ 很小，梯度也不会归零（因为 +1 项），确保了深层可训练性。二是多了一条通路

在 $H (x) = F (x) + x$ 这个结构的约束下下，使得 $F (x)$ 的学习行为，看起来像是在弥补 $x$ 和 $H (x)$ 之间的差距。对于单个层而言，它依然是在寻找最优的输出，但是因为整个网络结构的改变，反向传播的过程中，被 $H (x) = F (x) + x$ 约束，那么这个最优的输出就会的被动的被转化为 $H (x)$ 和 $x$ 之间的差距。

而这，也直接解决了恒等映射的根本问题。

假设对于某个输入 $x$ ，理想的输出 $H_{t a r g e t} (x)$ 就是 $x$ 本身，即恒等映射是最优的。

传统网络块: Output_block = F(x)。为了达到 Output_block ≈ x， $F (x)$ 必须被训练成一个近似的恒等函数。这对于多层非线性网络来说，并不平凡，权重需要非常精细地调整。

残差网络块: Output_block = F(x) + x。为了达到 Output_block ≈ x，优化器只需要将 $F (x)$ 的输出驱动向0。让一个网络的输出为0通常比让它精确地复制输入要容易得多。

所以，当深层网络中许多层实际上只需要执行近似恒等映射时，残差结构使得这些层可以轻易地将它们的 $F (x)$ 部分学习为接近0，从而让信息通过 +x 路径“无害通过”，避免了性能退化。

问题

add所产生的恒等映射一定是好的吗？

恒等映射可能的缺点

这种机制设计的初衷是在不需要复杂变换时提供捷径选项，而非让所有深层都“偷懒”。因此，如果深层网络中持续、普遍地发生恒等映射，则表明这些深层未能学习到有意义的非线性特征变换，网络的实际有效深度可能不足，未能发挥其深层结构的潜力。这通常是模型设计或训练优化问题的警示信号。理想状态下，健康的深层网络应选择性地利用恒等映射保护重要信息，同时在必要层进行有效的特征学习和抽象。

一个衍生问题：

为什么是add，而不是concat？

特征融合视角

这部分只是扩展，对于有基础的同学可以跳过

站在特征融合的视角下，在图也就是CNN和语言类（在这里，我们特指bert或者语言任务的transformer），实际的含义是不同的。

在transformer中，通常是这样表示三个维度(batch_size, sequence_length, feature_dimension)，也就是我们常说的(B, S, D)。那么数据传入到attention和FFN中是有具体含义的。

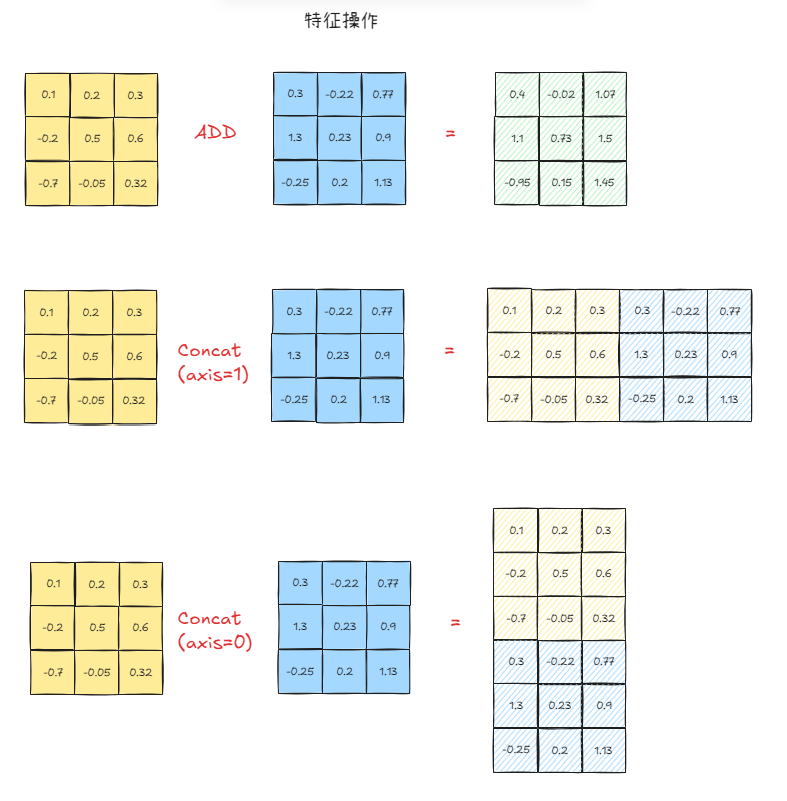
我们来看一下在二维视角下的add和concat操作。假设我们有一个二维矩阵，让我们先抛开Batch这个概念，只剩下[S, D]

add： 那就是两个3x3的矩阵对应的位置的逐个元素相加，结果仍然是一个3x3的矩阵。这是将两个特征融合到一起，但是维度不变。其缺点就是，我们把特征加一起了，某些情况下无法感知到原有特征是什么样的。
concat(axis=1)： 我们沿着水平方向拼接，得到一个(S, 2*D)的矩阵，在这里，就是3x6。特征翻倍了。这样做的好处是，我们的样本数量没变，还是3，但是我们的两种特征被原原本本的保留下来了。
concat(axis=0)： 这个情况比较特殊，在我们这个二维的例子上，它是错误的、无效的
- 因为纵向的堆叠，会给后续的层，造成错误的理解。他们本来他们是特征，然后因为我们顺着纵向堆叠。在我们刚才的意义上，纵向是S，也就是一个句子，如果堆叠起来，那对于下一个sublayer（无论是attention还是FFN）会错误的理解它为6个特征维度为3的句子。
- 但是这种拼接方式并非无用，它多用于数据处理阶段。还记得我们的(B,S,D)的结构么，batch_size就是这样沿着axis=0拼接而来。当我们有多个tensor，形状为[S, D]。就有了一个batch = concat([tensor_1, tensor_2, ..., tensor_N])这样操作之后，我们就有了N个[S, D]堆叠的数据，也就是我们熟悉的`[batch_size, sequence_length, feature_dimension]

特征操作

那么到这，基本上就事情就明朗起来了。如果不用add，我们就只能concat(axis=1)，因为concat(axis=0)在我们transformer这个部分会完全改变数据结构，让下一个层错误的处理。而concat(axis=1)会让我们的特征维度翻倍。当我们原始的shape是[B,N,D]，操作之后，就会变成[B, N, 2*D]的情况。而随着我们堆叠层数，最后这个 $2^{N}$ 会让我们的数据爆炸。

那么现在我们终于可以完整的回答为什么是Add?

Add：从反向传播的角度看，损失函数 L 对输入 $x$ 的梯度 $\partial L / \partial x$ 包含了 ∂L/∂Output * (1 + ∂Sublayer/∂x)。这里的 +1 项至关重要，它创建了一条无阻碍的梯度“直通路径”。这意味着即使 Sublayer 的梯度 $\partial S u b l a y e r / \partial x$ 因深度增加而趋于零，梯度信号本身至少能以 1 的系数无衰减地向前传播。

这从根本上保证了即使在数百层的Transformer中，底层的网络参数依然能接收到有效更新的信号。它假设 Sublayer(x) 的作用是学习对原始信息 $x$ 的一个增量 Δx。如果某个子层无益，网络可以通过学习将 Sublayer(x) 的权重趋近于零，使其退化为恒等映射 Output ≈ x，从而动态地调整模型的有效深度。

Concat：首先如果采用 Output = Concat(x, Sublayer(x))，则不存在这样的梯度直通路径。梯度必须完整地流经处理拼接后向量的后续所有层。在深层结构中，这会使梯度传播路径变得冗长且复杂，连乘效应将重新主导，梯度消失或爆炸的风险会急剧增加，这与构建深度模型的初衷背道而驰。

其次，拼接操作会直接导致维度扩张：dim(Output) = dim(x) + dim(Sublayer(x))。在Transformer中，这将导致维度变为 2 * d_model。如果连续堆叠，维度将以 d_model * 2^N 的形式指数级爆炸（N为层数）。

当然concat有自己擅长的领域，比如densenet，或者多模态融合的时候，当处理来自不同模态（如图像的CNN特征和文本的BERT特征）或不同来源的信息时，这些特征向量的语义空间和维度通常是不同的。在这种情况下，进行加法操作是无意义的（好比将像素值与词向量ID相加）。**拼接**是唯一合理的方式，它将不同信息源的特征并列，形成一个更宽的表征，交由后续的融合层（Fusion Layer）进行处理。

add操作就没有缺点么？

$F (x)$ 值过大的后果

add 有效的情况高度依赖于一个关键前提： $F (x)$ 的输出量级需与输入 $x$ 相匹配。

除了恒等变换，如果 $F (x)$ 和 $x$ 量级不匹配，换句话说，当 $F (x)$ 过大了，那就会引发新的问题。

首当其冲的是，信息流破坏： 若 $| | F (x) | | >> | | x | |$ ，则 $y = F (x) + x \approx F (x)$ 。此时，add 操作本应保留的底层特征 $x$ 被“淹没”，残差块实质上退化为一个普通的前馈层，失去了保护原始信息流的初衷。

其次是梯度流不稳定： 在反向传播过程中，梯度 ∂Loss/∂y 会等量地流向 $F (x)$ 分支和 $x$ 分支，即 ∂Loss/∂F(x) = ∂Loss/∂x = ∂Loss/∂y。如果 $F (x)$ 本身或其内部计算的梯度 (∂F(x)/∂θ) 过大（通常伴随大的 $F (x)$ 值），流向 $F (x)$ 分支的梯度也会异常巨大。这极易导致三个问题：

梯度爆炸： 过大的梯度在多层残差块中累积，引发权重剧烈震荡、更新步长失控，甚至出现数值溢出。

训练不稳定： 权重参数的剧烈波动破坏优化过程的收敛性，导致损失函数剧烈震荡，难以达到良好的局部最优点。

泛化性能下降： 不稳定的训练过程往往难以收敛到鲁棒的解，损害模型在未见数据上的表现。

为什么 $F(x)$ 会变得特别大？如何防止$F(x)$值过大？

$F (x)$ 值过大的常见原因

输出值过大是深度残差网络训练不稳定的核心风险，根本在于特征尺度在前向传播中未经有效约束而被逐层累积放大。

主要原因是缺乏批归一化 (BN) 或层归一化 (LN) 等机制，网络无法动态调整中间层激活值分布。的输出尺度会随网络加深逐层累积，最终导致数值失控。所以自然而然的，Add & Norm被一同提及。归一化它们将 $F (x)$ 约束到稳定分布，近似均值为0，方差为1。

初始权重过大，是另一个可能会导致 $F (x)$ 过大因素，不当的初始化，会导致信号在传播初期即呈指数级增长趋势。一般的解决方案是使用智能的权重初始化策略比如He或者Xavier。

过大的学习率也会导致权重更新步长失控，可能使 $F (x)$ 及其梯度在单次迭代中剧增，破坏数值稳定性。通常是使用 **学习率预热在初期使用小学习率稳定网络，随后提升；配合 学习率衰减在训练后期精细调整步长。

Norm

由于Norm是一个稍微大一点的章节，这里已经初步介绍了为什么Add & Norm经常一起出现。Norm的深度展开放在下次。

在基于 Transformer 的架构中，Add & Norm 通常作为一个成对出现的核心组件。

之前讨论过，归一化操作（如 Batch Norm 或 Layer Norm）的核心功能之一是防止激活值（F(x)）的尺度（Scale）在传播过程中过度膨胀或收缩。然而，其作用不止于此。

Add 操作（残差连接）本身会显著改变数据的分布。即使两个相加的变量（如输入和前层输出）具有相似的分布，它们的和也会形成一个新的分布。例如：

X \sim N (μ_{1}, σ_{1}^{2}) 且 Y \sim N (μ_{2}, σ_{2}^{2}), 则 X + Y \sim N (μ_{1} + μ_{2}, σ_{1}^{2} + σ_{2}^{2})

这意味着 Add 不仅改变了均值 $μ$ 更重要的是显著增加了方差 $σ$ 。数据分布的变化，尤其是方差的增长，会使得后续层的输入分布持续偏移。

此外，紧随其后的前FFN中的非线性激活函数，具有非线性的尺度变换效应。它们会基于输入值进行选择性抑制，比如经典的ReLU 将负值置零或 GELU 对正值进行近似线性的缩放，对负值进行平滑抑制。这种非线性变换会进一步扭曲数据的分布和尺度。

综合来说，Add 操作带来的分布偏移和 FFN 非线性激活的尺度变换效应叠加，会导致深层网络中数据的分布持续变化且尺度难以控制。而且这种变化是累积的，随着网络深度的增加，会指数级恶化。如果不进行Norm，后续每一层都需要不断地适应其输入的动态变化的分布和尺度。这不仅极大地增加了模型优化的难度，还容易导致训练过程不稳定和收敛速度变慢。

在标准的 Transformer 结构中，由于序列数据的处理是独立于 Batch 维度的，这种数据的特点是序列长度可变，不同序列间差异大，Batch Normalization 并不适用。因此，Layer Normalization 成为自然的选择，它作用于单个样本的所有特征维度上，不依赖于 Batch 统计量。

正是基于 Add 和 FFN 引入的分布与尺度变化问题，以及 Layer Norm 在序列模型中的适用性，Add & Norm 组合成为了 Transformer 及其衍生架构中不可或缺的标准模块。

结语

关于残差连接的优缺点和必要性介绍就到这了。接下来就该是Norm的演进和变化了。

参考

Huang, G., Liu, Z., Van Der Maaten, L., & Weinberger, K. Q. (2016). Densely connected convolutional networks. arXiv:1608.06993. Retrieved from https://arxiv.org/abs/1608.06993

He, K., Zhang, X., Ren, S., & Sun, J. (2015). Deep residual learning for image recognition. arXiv:1512.03385. Retrieved from https://arxiv.org/abs/1512.03385

苏辄. (2019). 如何理解神经网络中通过add的方式融合特征？. 知乎. Retrieved June 12, 2025, from https://www.zhihu.com/question/306213462/answer/693718385

Add & Norm：对残差连接深入解析（一）

作者phimes

发布于2025/6/12

更新于今日内

许可协议 CC BY-NC-SA 4.0

署名-非商业性使用-相同方式共享 4.0 国际

LLM 算法原理

反馈与投诉

Add & Norm：对残差连接深入解析（一）

写在前面 ​

Add & norm介绍 ​

transformer中的add & norm 代码 ​

信息差 ​

例子 ​

理解信息差 ​

网络退化（Degradation） ​

恒等映射（Identity Mapping） ​

问题 ​

恒等映射可能的缺点 ​

特征融合视角 ​

F(x)值过大的后果 ​

F(x)值过大的常见原因 ​

Norm ​

结语 ​

参考 ​

写在前面

Add & norm介绍

transformer中的add & norm 代码

信息差

例子

理解信息差

网络退化（Degradation）

恒等映射（Identity Mapping）

问题

恒等映射可能的缺点

特征融合视角

$F (x)$ 值过大的后果

$F (x)$ 值过大的常见原因

Norm

结语

参考